Diffie-Hellman Key Exchange Protocol
The Diffie-Hellman key exchange protocol is a secure way of exchanging a secret, for the sake of use with symmetric encryption. Note that this secret is not predetermined, and hence Diffie-Hellman is not useful for sending messages itself.
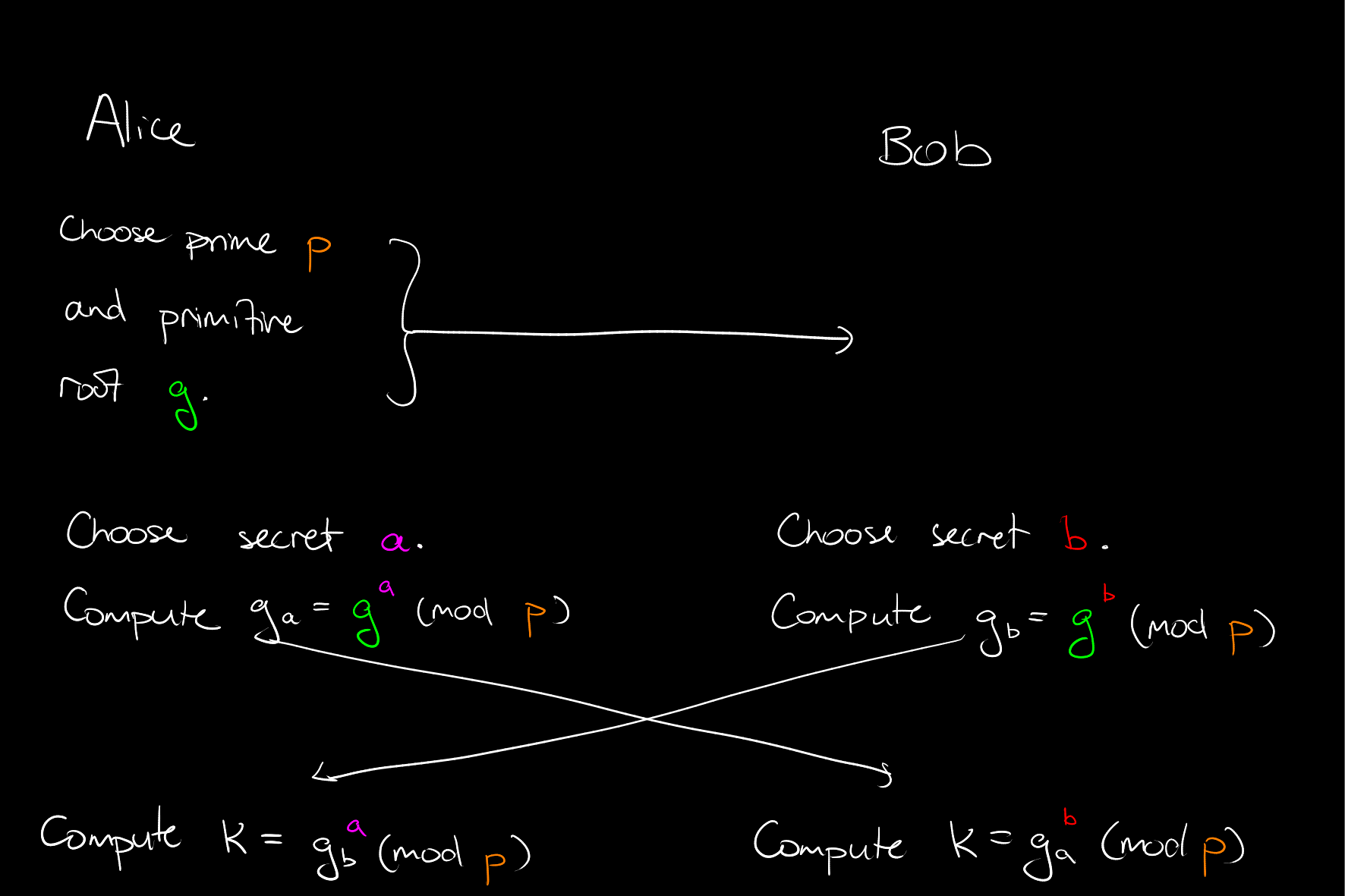
This algorithm requires two parties, \(A\) and \(B\).
Party \(A\) chooses a prime number \(p\) and primitive root \(g\) of \(\mathbb{U}_p\). Then both parties choose a secret integer \(a\) and \(b\) respectively.
\(A\) calculates \(g_a = g^a \mod p\), while \(B\) calculates \(g_b = g^b \mod p\).
\(A\) then sends \(g_a\) to \(B\) and \(B\) sends \(g_b\) to \(B\).
\(A\) then calculates \(K = (g_b)^a \mod p\), while \(B\) can calculate the same value \(K = (g_a)^b \mod p\). This value \(K\) is then the shared secret key.
Here is a diagram showing the procedure, which makes it clear which calculations are which party's responsibility, and exactly which data is sent (and therefore which data an evesdropper has access to).
It is clear that this process works as desired, since: